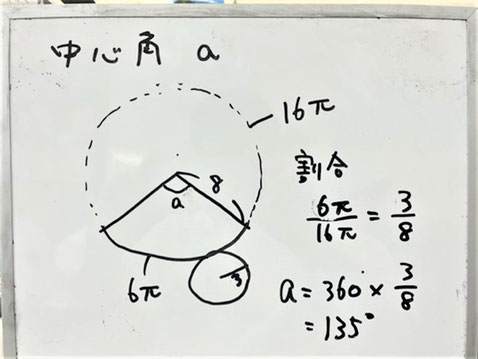
扇(おうぎ)の問題の考え方
📖
公式を使うのは、
その公式の意味がわかってから✋
中1数学🌸
こんにちは。
静岡学習塾の西ヶ谷です。
('ω')ノ
公立と私立では、
教科科目にちがい
あることを知ってましたか❓
(※例外あり)
たとえば、数学でいうと、
通常は数学という教科は
1つですが、
私立の学校の中には、
数学が2科目あって、
計算系の分野と
図形系の分野(幾何)
をわけて、
2科目としています。
つまり数学が2個👀
数学が苦手な人は
ひっくりかえりそうです。
苦笑
当塾でも、数学が2科目ある
学校の生徒さんが
おられます。
そんなケースでは、
数値や文字式の計算をしたり、
かといえば、
面積や体積を求める
ような問題も
同時併行で進んでいます💦
そこでですが、
今回のテーマは、
その図形の分野で、
「扇形(おうぎがた)」
について、
塾でやったことを
再現してやってみたいと思います。
※扇形:円の2つの半径と
弧で囲まれた図形のこと。
Let’s get started👉👉👉
(さあ、始めましょう)
円錐(えんすい)の問題
(空間図形)
で、展開したときの
形について、
(展開図)
質問されることがよくあります。
円錐を展開すると
図のように扇と円に
なります。
そして、
そのときの面積や
弧の長さや
扇の中心角の大きさを
求めよ👊
っていう問題は、
定番です✋
この問題を簡単に通過
できる生徒さんって、
あんまりいません👋
それだけ、考えさせられる
ってこと。
それでは、
塾の生徒さんにお教えした
ときの
実際のホワイトボードを使って
お話を進めたいと思います。
【問題】
底面の3cm
母線8cm
(円錐の頂点から底面の
円の円周までの長さ)
の円錐の展開図について、
扇と円の面積比を求めよ。
💁♀️
てな、問題でした👐
🌸最近のブログ
わからないときに「調べる」のが勉強👈push😲
過去問をやっておけば大丈夫なの?👈push😲
地理を教えます。👈push😲
一冊を完璧にする パート2👈push😲
一般動詞の過去形は簡単なのですが・・・中1英語👈push😲
小テストでいきなり満点をとると先生は見てますよ👈push😲
一冊を完璧にする! パート2👈push😲
やるべきことは先にやる。先手必勝!👈push😲
面接では正直に話す (中学受験面接練習より)(👈push😲

コメントをお書きください